Project
The Center will focus on the development of new techniques and tools for mathematical modelling and the analysis of large ordered complex systems.
The primary scientific objectives are as follows:
- Leverage the recent developments in data science to build mathematical models for large ordered complex systems that are typically difficult to model from first principles. Some examples of such systems include models for climate systems, biological systems and complex flows.
- Development of network-based techniques, that are built on rigorous mathematical foundations, for the analysis of such complex systems.
- Investigate reduced order modelling strategies that enable reduction in computational costs without compromising the accuracy of the predictions.
- Development of data driven approaches for estimating model parameters for the above approaches from measurements and observations, so as to be applicable to physical problems.
Apart from the scientific objectives, the formation of the Center is expected to show the following intangible but significant outcomes:
- To provide legitimacy to initiate collaborative research on dynamical complex systems with international groups in a more structured and formal manner.
- To increase collaborations among faculty members within IITM, enabling joint funded projects as well as, joint research guidance. While presently this is still possible, being affiliated to a Center will provide a structure and impetus.
- Tie-ups/MOUs with international groups for joint research programs and personnel (research students, post-docs, faculty) exchange.
- Host international experts as visiting faculty for short durations; offer short term courses and seminar series, under the aegis of the Center.
- Hire international postdocs, YIFs under the aegis of the Center.
- Organize thematic international schools/workshops on a regular basis and at least 1 big international conference in the next 5 years.
- Create and run an Interdisciplinary Dual Degree (IDDD) Program on Complex Systems and Dynamics. (this has already been started link)
- Start an undergraduate minor/honours program in Complex systems.
- Develop a robust research program (MS/PhD/DPhD).
- Promote the growth and awareness of Complexity Science in the country.
Thrust Research Directions
The activities of the Center will be carried out under several verticals, all of which are interdisciplinary in nature and require expertise from varied disciplines. Some of the key areas in which the activities of the Center will be focussed in order to meet the stated objectives are as follows:
Complex Networks
Complex systems consisting of a large number of interacting elements are efficiently modelled as a network of these individual elements. Examples of such systems include biological systems like neuronal networks in brains and gene-regulatory networks in biological cells, ecological systems such as fish shoals, locust swarms and bird flocks, technology induced systems involving communication, energy and computation networks, social systems and climate systems. Techniques developed for the analysis of networks include synchronization, the study of topological characteristics, construction of time series networks, stochastic processes, random graph theory, and queuing theory. New network and topological techniques for the analysis of time series have been developed by members in this group, which have the potential for applications in a host of complex systems, including climate, neurological networks, swarm dynamics and biomimicry, epidemiology, complex fluids and multi-physics systems.
Spatiotemporal dynamics of extended systems
The study of nonlinear dynamics and chaos has been traditionally a strong area in IIT Madras. However, gaining insights into the behavior of complex systems requires investigating the dynamical behaviour of the networked system and its bifurcation characteristics. This is essential to develop a deeper understanding of the physics associated with the problem, and identifying precursors for dramatic events that can have far reaching consequences. The application areas include climate, biological and social complex dynamical systems.
Stochastic modelling and probabilistic approaches
Mathematical modelling of complex dynamical systems are based on simplifying assumptions, measurements of varying resolutions spatio-temporally and often incomplete knowledge of the system and its parameters. Moreover, the need for modelling the inherent inhomogeneities that invariably exist in the subunits of a networked system implies the need for stochastic modelling and adopting probabilistic approaches in the subsequent analyses of the complex systems. This requires development of more sophisticated techniques for the analysis and for the interpretation of the system dynamics
Causal Discovery of Complex Systems
Industrial, biological and several large-scale processes in other domains involve complex interconnections of subsystems, the knowledge of which is often unknown a priori. Further, the directionality of inter-variable and inter-system connectivities, the causal maps, are often directly not known due to limited or no understanding of the underlying mechanisms. Modern data science and analysis techniques offer powerful tools for discovering these causal relations from the process measurements. Causal discovery has been a hot area of research in neuroscience, computer sciences and more recently in engineering for reconstructing networks and causal maps for complex processes with ideas originating from econometrics and social science. Data-driven causal inference is useful even when a first-principles understanding of the connectivity is available since it allows us to determine the “effective” connectivity under the given operating conditions. Applications of causal discovery include inference of effective connectivity from EEG and fMRI data, reconstructing dynamical process networks of industrial plants from routine measurements, discovering social networks from social media data and reconstructing climate networks, to mention a few. These problems are highly challenging and intriguing due to the interplay between the deterministic and stochastic characteristics of process and measurement mechanisms, non-linearities involved, sensing requirements, large-scale computations and other standard issues associated with data-based approaches. The lack of a mature theory for formal definitions of causal connections, diversity of theoretical possibilities and a yet-to-mature unified formalism of graphical representations for dynamical representations makes this area of research highly fluidic as of date. A sound theoretical framework that accommodates diverse definitions of causality for dynamical deterministic and stochastic systems, a set of efficient, robust and computationally scalable inference methods along with appropriate graphical representations of the derived knowledge are the most demanding aspects of research in this area. A host of applications stand to benefit from the outcomes of research in this field.
Bio-complexities and dynamics of biological & bio-mimetic systems
Biological and biomimetic propulsion systems across widely different length scales pose many interesting challenges. Understanding the secret of their superb locomotion capabilities requires a multidisciplinary approach; the roles played by the multiple key elements in the complex flow-field in dictating the loads and paths of individual agile objects and in controlling their maneuvers are still largely unknown. Secondly, predicting the collective activities of swarms, flocks, dense human crowds, schools, of a wide spectrum of such propulsion systems is yet another crucial problem in complex dynamics. The natural organization of species of insects, birds, fishes and even human crowds are robust and flawless, and inspire the design of bio-mimetic devices for various futuristic applications. The aim is to predict the individual propulsion and associated complex fluid dynamical patterns, as well as interactions between different individuals elements leading to a range of collective behaviour like alignment, polarization, aggregation, swarming etc., with confidence. Dynamical models and networking algorithm-based models could be utilized effectively in capturing the qualitative and quantitative trends of the collective patterns of species. Recently, large volumes of data on collective behavioral patterns, which were not available historically has started to come in from realistic experiments, that can be useful in benchmarking and validating the emergent complex algorithms and can also be exploited to propose data based predictive tools utilizing algorithms from the realm of artificial neural networks. Expertise on these areas can come from Computer Science, Electrical engineering, Physics, Aerospace engineering, Mechanical engineering and Applied Mechanics departments.
Studies on biological dynamical systems are essential to understanding the behaviour of animals and small organisms. At the crossroads of biological physics and mechanics lies the fascinating field of physics of living systems. Groups in Physics, Chemical Engineering and Applied Mechanics department use ideas from non-equilibrium statistical mechanics and hydrodynamics to model the collective behavior of active matter. These studies are also crucial for resolving the dynamical behaviour of futuristic bio-mimetic and biomedical devices and their interaction with the environment. The analyses of problems like the physics of insect flight, or swarming behaviour are other problems, which are relevant to this area.
Subprojects under the pCoE (details about each in later slides)
- Climate Networks – Neelima Gupte, Sunetra Sarkar, Elena Suriovyaktina
- Stochastic modeling and machine learning in climate science – Anubhab Roy, Sayan Gupta, Woosok Moon
- Stochasticity and noise induced transitions in spatio-temporal systems – Sayan GuptaAnubabh
- General oscillatory neural network models to understand fMRI data – Neelima Gupte, Srinivas Chakravarthy, Sayan Gupta
- The analysis of bird song – Neelima Gupte, Srinivas Chakravarthy, Gabriel Mindlin, Ana Amador
- Complex networks of multiphysics systems – Sunetra Sarkar, Didier Lucour
- Physics informed machine learning surrogates for complex flows – Sunetra Sarkar, Diider Lucor, Muraliu Damodaran
- Physics of living matter – Sumesh Thampi, Anubhab Roy, Vivek Prakash
- Dynamic network modelling of human breathing – Mahesh Panchagnula
- Urban climate modelling – Sunetra Sarkar, Didier Lucor, Kirti Rajagopalan
- Swarm dynamics- Sayan Gupta, Sunetra Sarkar, Mahesh Panchagnula
- Dynamics of social behaviour – Sayan Gupta, Mahesh Panchagnula, Sarah Wolf, Madhav Marathe
- General inference for climate network reconstruction and process oriented model evaluation – Arun Trangirala, Udit Bhatia, Auroop Ganguly
- Reconstruction of causal dynamical networks of industrial processes- Arun Tangirala, Biao Huang
Project 1: Climate Networks
The climate system is a highly complex nonlinear system and one way to approach such a system is by constructing a complex network from massive datasets and weather observations. Such a network can be constructed for the climate system by assuming that the climate system is represented by a network, with each node representing a geographic location at which climatic time-series data is available. Links are constructed between the nodes based on the correlation between the time series at the pairs of nodes.
Tools of statistical physics will be applied to these networks to analyze the structural changes in the network and construct an order parameter which can be used to forecast some important climate phenomena, such as the monsoon, the North Atlantic Oscillation and El Niño events. Such systems can have tipping points at which a phase transition to a contrasting dynamical regime occurs. Finding the precursors of such critical points before they occur is important and difficult.
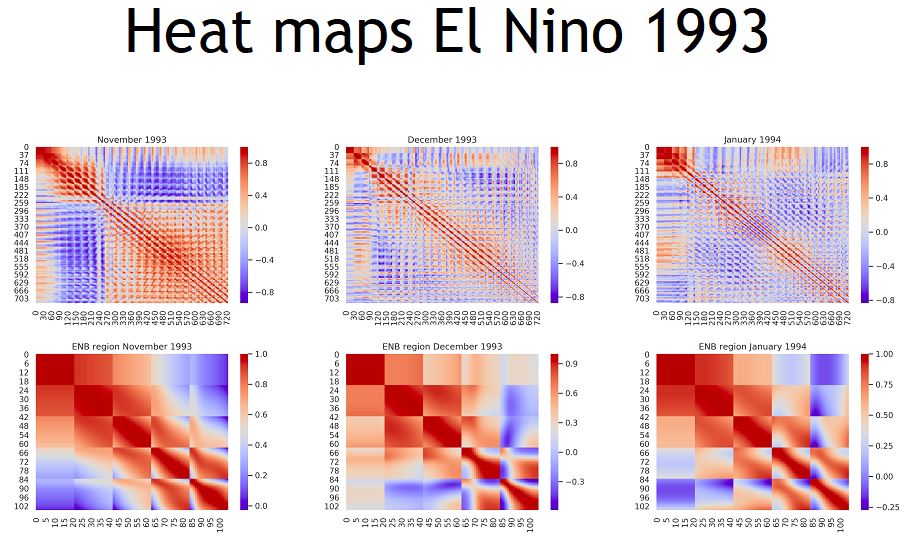
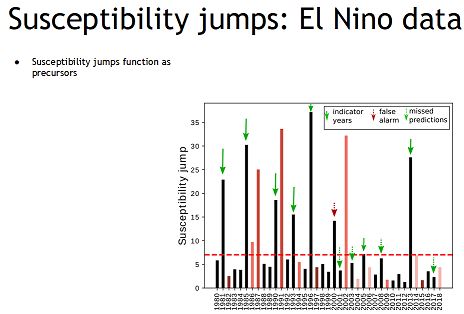
Frameworks of percolation theories will be used to analyze the order parameter and the susceptibilities to find the precursors of the tipping points. The density, distribution and geographic location of the links of the network can also shed light on the links, locations and teleconnections, which are important for climatic phenomena. The objective is to identify tipping points for these events, analyse the differences between these and events like the La Nina and pin down the role of teleconnections. Use of tools such as heat maps, clustering quantifiers, recurrence networks and investigating their reliability for identification and prediction of these and other climatic events will be undertaken.The dynamics may also be interpreted as a multi-attractor system in the phase space and stochastic perturbations may randomly switch the response among different attractors. A recurrence network based model can closely reflect the topological structure of the corresponding state space and the network measures can capture the changes in the dynamics as key environmental parameters change. It is of interest to estimate measures like global clustering coefficient and characteristic path length. The scale-free nature of the network can also be investigated.
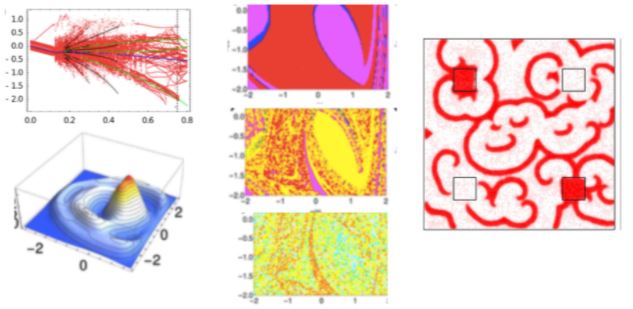
Figs below: Cyclone Vardah (6-18 Dec. 2016) Cyclone Nada (29 Nov -2 Dec 2016) (Order parameters and susceptibility)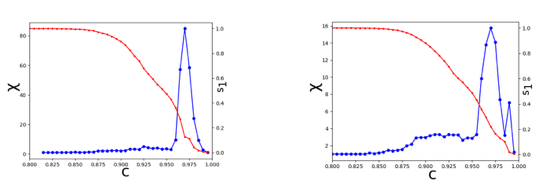
Project 2: Stochastic modelling and machine learning in climate science
Despite the enormous progress in the development of Global Climate Models, resolving the complex spatio-temporal processes with appropriate resolutions is far from satisfactory. Complementary approaches based on the development of stochastic models provide alternative computationally cost-effective techniques to investigate and predict the dynamics of the climate system. In this research, we propose to build on these existing studies and employ machine learning algorithms on these problems.
Stochastic perturbation theory A perturbation method for the periodic, non-autonomous 1D stochastic differential equation has been used to investigate the seasonal variability of Arctic sea ice to find out the essence of the seasonal variability using the relationship between the seasonal stability of Arctic sea ice and weather-related high-frequency processes. We propose to expand this method for more general situations, including higher dimension and generalised noise forcing. One of the examples is El Nino-Southern Oscillation (ENSO) represented by stochastic recharge model, which is a 2-dimensional dynamical system. The model is generalised to include the seasonality of Bjerknes feedback to represent ENSO’s phase locking and the consideration of multiplicative noise forcing is expected to explain the cause of the asymmetry of the ENSO statistics. The extension of the perturbation theory to higher dimensional system could be applied to the ENSO variability research. The further development of stochastic perturbation theory for various periodic non-autonomous stochastic systems will be able to open up many directions of applications in climate science.
First passage, extreme events and critical behaviour Questions of public interest related to climate change such as, when would the summer Arctic ice disappear completely, the effects of climate change on the frequency of flooding in Chennai or whether the climate system is close to the tipping point, can be addressed only probabilistically. For this one needs to use theories of stochastic dynamics. The first question regarding the timing of Arctic sea ice extreme status can be posed as a problem in first passage time. The second one is related to the statistics of rare events and the last one to the characteristics of the stochastic solutions near a bifurcation point. These theoretical problems, which have been widely considered in autonomous stochastic systems, will be generalised to the periodic non-autonomous stochastic models to answer the above public inquiries.
Complex networks for seasonal variability The stochastic model represented by a single 1D differential equation is not sufficient to contain various teleconnections in climate. An alternative is to develop complex network models based on the existing 1D stochastic model with the inclusion of coupling terms. Recently, the coupling function, which has been introduced to reveal the interactions of underlying processes such as synchronization, has been introduced to investigate the mutual in between ENSO and IOD (Indian Ocean Dipole). We propose to consider the expansion of the two-dimensional stochastic model towards a multi-dimensional one containing interactions among many distant areas. In seasonal time-scales, the network model is expected to reproduce the seasonal statistics contained in data and provides information about how the multiple agents in the network are influencing each other.
Hybrid of stochastic model and deep learning Deep-learning algorithms such as Convolutional Neural Network (CNN) and Recurrence Neural Network (RNN) are being used for near-future predictions. The CNN and RNN are applied to a given time-series and produce a future prediction with an optimal choice of hyper-parameters inside the networks. Instead of using the original time-series directly, we propose to consider a stochastic model from the given data, the deterministic component of which represents slowly-varying processes and the stochastic forcing models the contribution of short-time processes. Assuming that the deterministic forcing is known, the noisy fluctuations can be retrieved from data. We can apply deep learning algorithms to the retrieved noise. Recently, it has been shown that this scheme is beneficial in predicting rare events, based on data containing no rare events.
Project 3: Stochasticity and noise induced transitions in spatio-temporal systems
Nonlinear dynamical models are highly sensitive to the model parameters that are estimated from observations having varying spatial resolutions. The uncertainties in modelling are incorporated into the mathematical model as noise. The effects of noise may lead to sudden and irreversible change in the system from one dynamical stable state to another, leading to sudden dramatic qualitative changes in the system dynamics, often leading to catastrophic events and are irreversible. It is of interest that these catastrophic events, classified as noise induced transitions, are predicted apriori for natural, biological and engineering systems.
While studies on noise induced phenomena have been investigated for low order systems, similar studies on large ordered networked systems are few and are of recent vintage. This study will focus on the dynamical long term features of noise induced behaviour on large ordered networked models. Some of the challenges involved would include developing reduced order models for the characterizing the dynamical features of such large ordered networked systems. Interestingly, studies carried out in the group on engineering systems have revealed that noise plays an important role in developing precursor measures to identify impending transitions; this aspect of the study will be investigated with respect to climate models as well.
Project 4: General oscillatory neural network models to understand fMRI data
There has been a lot of recent effort to model fMRI data using deep neural networks. However, these approaches only model time-averaged responses. For modelling spatio-temporal responses of the brain we need dynamic neural network models. We have recently developed a general, trainable oscillatory neural network model that can be used to learn time-series data. The model consists of Hopf oscillator expressed in complex-variable domain. Specifically, it was used to learn multi-channel Electroencephalogram (EEG) data accurately. In this project we plan to further extend the oscillatory network to model fMRI data also.
The above model will be developed into a class large-scale models of brain dynamics similar to The Virtual Brain (TVB) model, with some important differences. The TVB model principally uses neuronal mass models like the two-variable nonlinear oscillatory models including Fitzhugh-Nagumo model, Winson-Cowan model, Wong-Wang model, Brunel-Wang model, Jensen-Rit model, Stefanescu-Jirsa model, which can exhibit excitable dynamics and limit cycle oscillations. In these models, the oscillators are coupled by only one variable, which is analogous to “real-valued” coupling. They are trained by global optimization algorithms that adjust the coupling strengths so that the output of the oscillatory network matches the recorded brain dynamics. Furthermore, most of them do not have an explicit natural frequency as independent parameter which is trainable depending on external input signal. On the contrary, our modelling approach based on complex-variable formulation involves more biologically plausible learning algorithms. Thus it is more feasible to apply our modelling approach to not only explain brain dynamics data (eg fMRI or EEG) but also to explain behavioural responses.
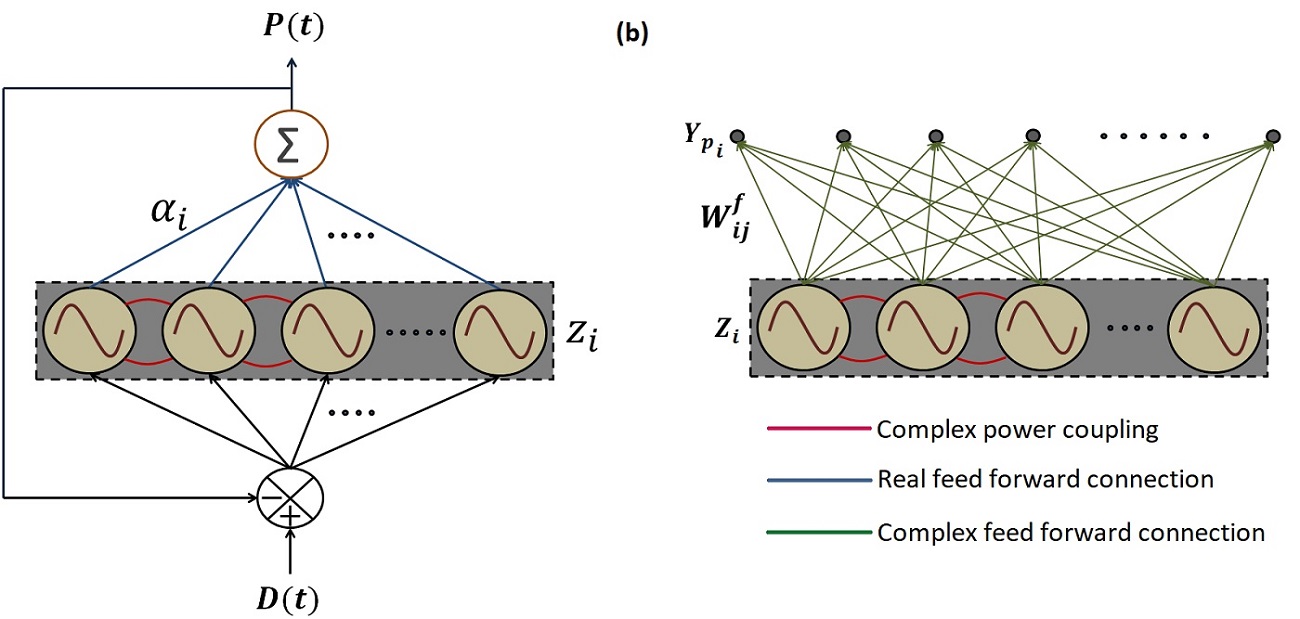
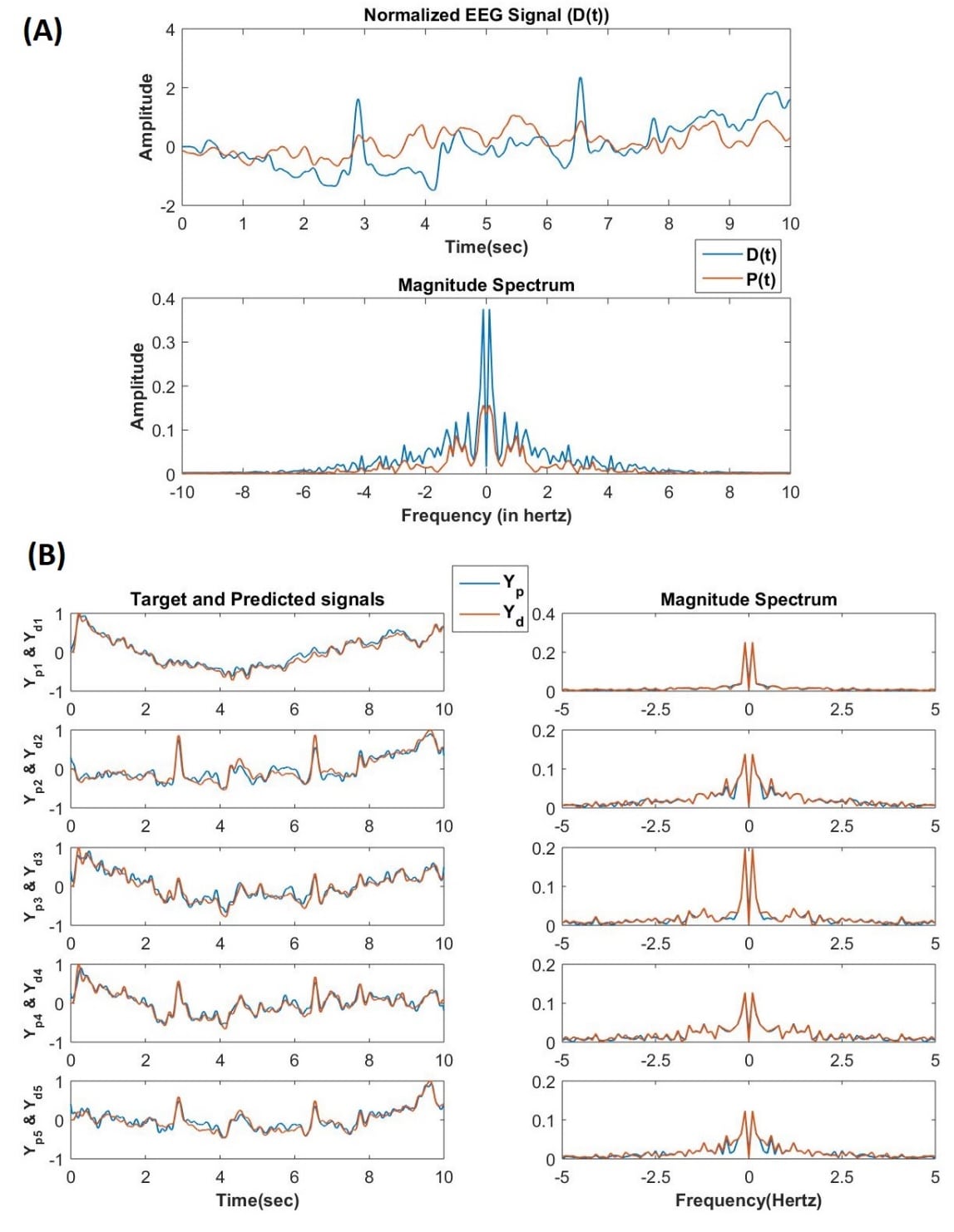
Project 5: The analysis of Bird Song
The activity of birdsong constitutes an important example of a process in which a neurophysiological process results in complex audible output. The study of the characteristics of the birdsong, and the identification of a system which can produce a synthetic birdsong of the same characteristics, provides important insights in the ways in which the neural architecture in the brain can coordinate with a delicate vocal apparatus that the bird can and must control with high precision. This study intends to deal with the physical mechanisms at work in the production of birdsong, the acoustic effects that the avian vocal organ is capable of generating, and the nature of the neural instructions that are needed to drive it. In addition, bird-song shares with human speech the feature that the acquisition of vocalisation matures with age and also requires exposure to a tutor.
The tools required for this analysis draw from multidisciplinary areas neuroscience, dynamical systems, time series analysis, and recently, machine learning techniques and optogenetics. We hope to analyse the elements of bird song as well as the changes which occur in the structure of the birdsong in the development of the bird using tools such as Hurst exponents, simplicial characterisers, multifractals and complexity measures. We hope to draw on expertise on time series analysis and nonlinear dynamics (N. Gupte, G. Mindlin) , neuroscience (V. Srinivas Chakravarty, G. Mindlin) and machine learning (V. Srinivas Chakravarthy). We hope this activity will grow and we will be able to involve experts on optogenetics and machine learning.
Project 6: Complex networks for multi-physics systems
Multi-physics systems represent complex interactions between several member systems whose coupled nonlinear and stochastic behaviour dictate the overall dynamics and stability of the parent system. It is absolutely necessary to study all the member systems together through strong nonlinear interactions as loss of stability in such systems may cause significant damage or complete loss of control. Not only large scale fluid induced engineering systems, but small scale bio-mimetic devices may also qualify as good multiphysics candidates. These systems are often bi-stable and the unsteady flow-field with or without random fluctuations adds to their complexity as it introduces multiple spatio-temporal scales. In this study, we propose to characterize flow-structure interaction systems with subcritical nonlinearity using complex networks to characterize the dynamical states and predict instability. A network will model the complex system with heterogeneous connectivity, which represents the dynamics of the coupled-physics complex problem and properties that quantify the topology of the network can be used to characterize the dynamics. Time-series networks preserve the topological structure of the phase-space and the network measures characterize the dynamics and reflect the changes in system evolution as control parameter changes. The networks seem to have high global clustering coefficient and low values of characteristic path length that also points towards the small- worldness of the networks. A detailed parametric analysis under the network modelling will be undertaken subject to both additive and parametric stochastic fluctuations and the scope of the modelling in predicting impending instabilities and exploiting maximum dynamical-state information will be investigated.
The proposed investigation would have the following two broad objectives:
i) Leverage the recent developments in data science to build mathematical models for large ordered complex systems,
ii) Development of network-based techniques, that are built on rigorous mathematical foundations, for the analysis of such complex systems.

Figure: (L to R)Multi-physics fluid-structure system, Flow around structure, Recurrence network for a fluid-structure system
Project 7: Physics-informed machine learning surrogates for complex flows
Artificial neural networks (ANNs) are models inspired by natural biological neural networks. The related algorithms are part of deep learning where extremely complex representations can be learnt from data through artificial neural networks with multiple hidden layers of neurons. Multi-physics and complex flow problems often require one to obtain the spatio-temporal dynamics of the system for a large parametric space. Such problems become computationally intensive and becomes costly. This highlights the need for efficient, fast, accurate numerical solvers, accurate and highly reliable reduced order models and cost effective methods to solve inverse problems. With recent developments in general purpose GPU computing hardware and its massive parallelizability, we have been able to achieve significant acceleration of our existing numerical methods. However on the inverse problems front, they still would prove costly for complex non-linear dynamical/stochastic dynamical systems. Machine learning has proven to be effective in solving various pattern recognition problems in domains like computer vision and image processing, biomedical engineering, time series analysis, etc. Deep learning (DL) is essentially a subset of Machine learning where extremely complex representations/features can be learnt from data through artificial neural networks with multiple hidden layers of neurons also called a Deep neural network. Deep neural networks have been proven to be universal function approximators in the sense that they can approximate any measurable function up to any desired level of accuracy, however, the downside is its need to work with large amounts of data. Given the fact that large data acquisition of real engineering systems for inverse problems is costly, a new paradigm has emerged to integrate the physical laws and machine learning such that learning in small data regimes and solving forward/inverse problems of physical systems become possible. The emerging trends in this physics-informed neural network (PINN) approach for improving predictions, parameterization/model order reduction (MOR), forward solving of partial differential equations, inverse modeling & discovering of governing equations.



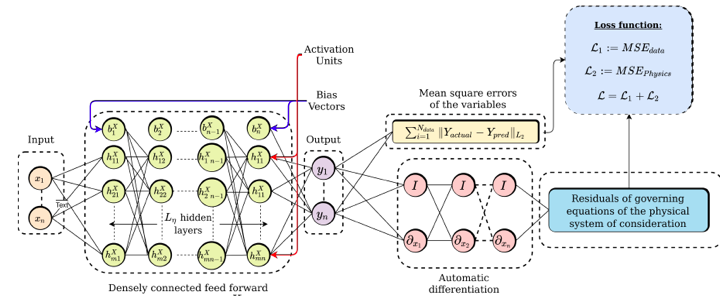
Figure: (a) Complex vortical flow-field, (b) Generic architecture of physics informed neural network
Project 8: Physics of living matter
Self-driven units, living or nonliving, capable of converting stored or ambient free energy into sustained states of motion comprise what is commonly known as active matter. Initial studies in active matter were focused on the motility behaviour of living cells like bacteria, algae, sperm cells; motivated by interests in biological physics of reproduction, infection and marine ecosystems. The scope has since been significantly expanded to include inanimate counterparts like granular rods and catalytically active colloids. These are non-equilibrium systems and are known to exhibit a high degree of collective behaviour due to their mutual interactions. Even in an isolated state, an active particle is a fascinating case study in dynamical systems. Their swimming expeditions often occur in an aqueous medium in torturous and deformable geometries leading to intriguing motile states; for example, mammalian sperm cells swim upstream through a long and complex female reproductive tract against a gentle flow to initiate successful fertilization. The hydromechanics of locomotion for various microswimmers could occur via either flagellar or ciliary propulsion.
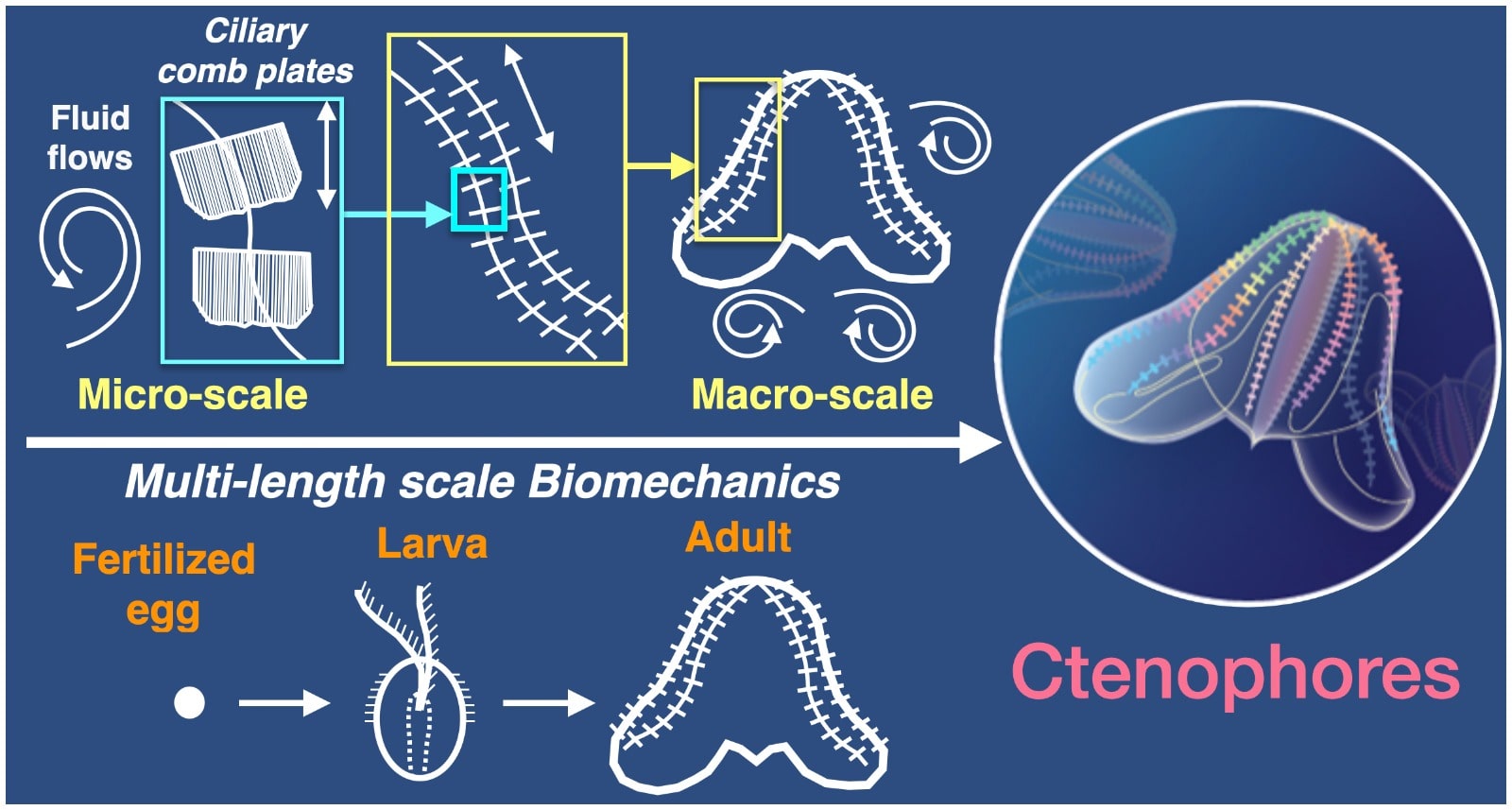
In the proposed study we will investigate ciliary propulsion across different length scales using a combination of experimental, theoretical and simulation approaches. The model organisms for our study would be marine invertebrates from the phylum - Ctenophora. Ctenophores are transparent, gelatinous marine animals that have eight rows of giant comb plates (ctenes) – which consist of the largest known ciliary structures (~1mm). These cilia are exploited for both motile and sensory functions. We plan to link the micro-scale ciliary biophysics to macro-scale behavior using both theoretical and experimental fluid mechanics approaches.
Our focus is on understanding ctenophore biomechanics: ciliary control, natural behaviors such as locomotion, predation, development and diversity. Our approaches would involve
Experiments - Laboratory studies will be carried out on the coastal Atlantic species Mnemiopisis Leidyi, one of well-known Ctenophores [8,9]. We study the fluid mechanics of locomotion and predation on three length scales: (1) microscopic scale to obtain high resolution flow-fields near the cilia (1-10 mm), (2) macroscopic scale to determine flow-fields around an individual (10-20 cm), and (3) collective scale to obtain flow-fields interactions around multiple individuals (> 20 cm). In addition, we will develop a new multi-scale technique that will allow us to measure fluid flows at all three length scales simultaneously.
Mathematical modelling - The ciliary propulsion of M. leidyi occurs in different fluid mechanical regimes, from low to intermediate Reynolds numbers, during their life cycle from the larval to the adult stage. Most theoretical studies on ciliary propulsion have focussed on low Reynolds number locomotion (Taylor’s swimming sheet and Lighthill/Blake’s squirmer). Using matched asymptotic expansions, we will develop analytical models for ciliary propulsion inclusive of fluid inertia effects.
Numerical simulations - Numerical simulations will complement the experimental and theoretical approaches associated with biomechanics of M. leidyi, linking the important physics observed in experiments but without other approximations that would be made in mathematical modelling. We will use lattice Boltzmann method (LBM) based simulations to study the ciliary locomotion of our swimmer at arbitrary Reynolds number. Lattice Boltzman method is a numerical technique to solve fluid dynamics by discretizing the Boltzman equation, unlike conventional methods where the exact governing equations are discretized and solved. LBM is widely popular to simulate particles of different shapes in a variety of complex geometries and background flows. Flow physics at all three length scales can be investigated using LBM. The flow due to a single cilia can be simulated using a flexible filament model while that due to an individual and multiple swimmers can be probed using the Lighthill/Blake’s squirmer model. The former is challenging in terms of coupling the momentum transport between a flexible filament and the fluid, while the latter is simpler as a slip-velocity can be imposed on a rigid particle. The moving boundaries in both the cases would continue to be challenging numerically, however LBM provides methods to tackle such issues.
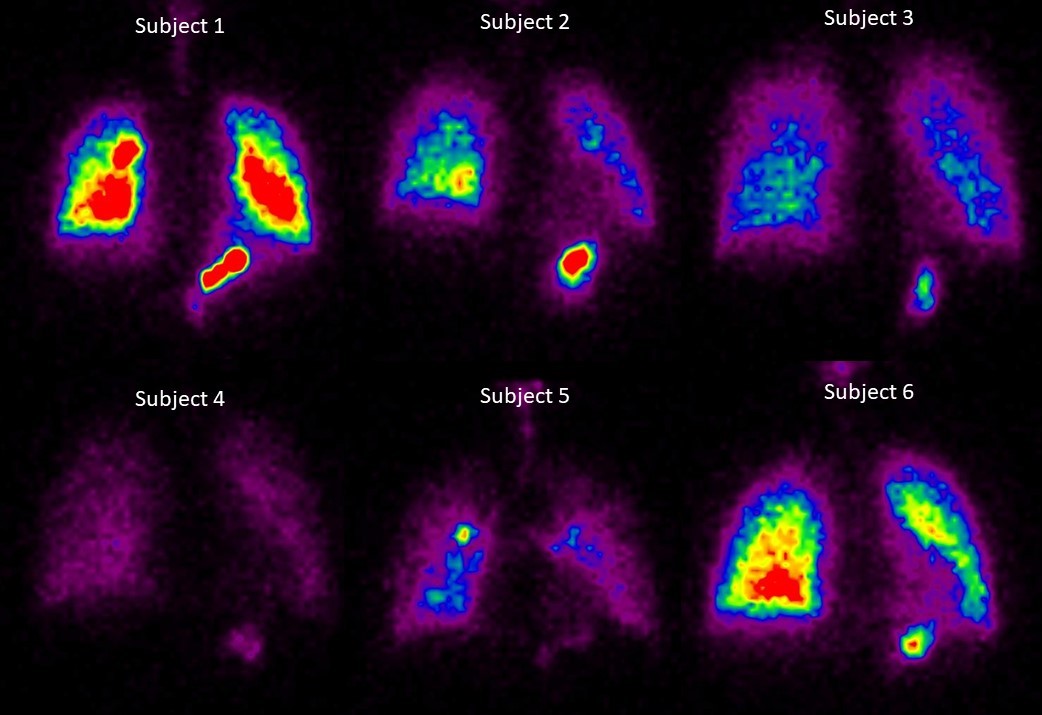
Project 9: Dynamical network modeling of human breathing
Human breath is a complex fluid flow that flows from the nasal passages through to the alveoli. During the course of such transport, the flow passes through a range of Reynolds spanning nearly five decades. Accompanying transport of aerosolized medicine or disease-causing droplet nuclei are influenced by the characteristics of this flow field. It is well known in the medical literature that subjects who are exposed to the same inhaled aerosol load (say virus-laden bio-aerosols) may show vastly different propensity towards infection. In a recent set of experiments from the PI’s lab, a small cohort of physiologically identical subjects exposed to a standard dosage of radio-labelled aerosol showed a factor of three variation in aerosol uptake.
The origin of this variability is as yet an unsolved problem in the literature. In addition, first principles modeling of whole lung flow, even if not including aerosol transport, is beyond the reach of today’s computational power. As a result, the best recourse is to invoke the power of network theory with reduced order fluid dynamic models. The lung lends itself to such an approach naturally, as it is a physical branching tree of bronchioles. During this study, we will study this problem using three complementary approaches.
Dynamical network model of the breathing process will be developed.
Experiments on an expanded cohort of human subjects as well as detailed experiments on phantom branching networks to provide model parameters.
Extreme value statistical principles based analysis will yield insights into “short-circuit” pathways that could accelerate progression to disease.
A dynamical network model of the breathing lung will be developed to simulate the flow of air through the lung during inhalation and exhalation. A parasitic model for aerosol deposition will also be coupled. Finally, this coupled model will require parameters that are lung-specific. Such parameters will be extracted from desktop phantom bronchiole experiments where aerosol deposition will be measured using spectrometric techniques. Once the model is developed and populated with human lung relevant parameters, it will be exercised to test out a hypothesis related to the pathways that disease causing germs take to reach the bloodstream. The lung is mostly a symmetric branching network. However, preliminary simulations have shown that a small asymmetry in the branching structure is likely to have a significant effect on the aerosol concentration that reaches the blood barrier in the acinus. It will be hypothesized that broken symmetry will result in “short circuit” pathways, which are paths of least resistance; subjects with increased probability of short circuits will show a greater propensity to become diseased. This hypothesis will be investigated using extreme value statistics principles.
Project 10: Urban climate modelling
Studies on urban microclimate are expected to grow rapidly in the near future and it is of interest to engineers, urban planners as well as policy makers, and coupled with the problem of pollutants’ spread and the related human behaviour, it becomes a complex problem overlapping the realms of physical and social sciences. The numerical approach employing high fidelity tools to solve the flow governing equations is increasingly becoming reliable as computational resources become better and cheaper. It is also largely due to their capability to handle urban geometries in detail and also the flow-field with high spatio-temporal resolution. It has already been employed with good success in the recent past with a focus on predicting urban heat-island phenomena [2] and spread of pollutants [3] but there is a need to widen the scope of these investigations and look at the transfer of the gained knowledge from climatology to planning and design. This will also require information exchange between multiple numerical frameworks.
Utilisation of experimental data in this context is also another area that has been largely overlooked, this is important not only for validation of the simulation/prediction tools but also for developing data driven machine learning platforms [4]. Prediction of urban climatology that involves costly simulations through complex geometries is an ideal application area for physics informed machine learning tools for future prediction and development of reduced order models [5]. Also, even though high fidelity simulations on microclimate studies are becoming popular, most of the studies are still available for cities belonging to the developed countries. There is a need to leverage on the existing expertise to study the urban scenarios in developing countries like India.
A discrete Lagrangian approach such as Agent-Based Modeling (ABM), which is an effective tool for modeling populations of adaptive individuals interacting with one another as well as their environment [6] can be combined with the high fidelity flow-field solvers [7] to develop novel hybrid platforms [7] to address the problem in its full complexity and get improved risk assessment and preparedness. Such hybrid platforms will be instrumental in simulating the behaviour of spatially-distributed populations of agents in the face of a physically realistic contaminated environment (flow-field).
Broad scientific objectives:
The above study will address the following broad scientific objectives
Leverage the recent developments in data science to build mathematical models for large ordered complex systems that are typically difficult to model from first principles. Some examples of such systems include models for climate systems, biological systems and complex flows.
Investigate reduced order modelling strategies that enable reduction in computational costs without compromising the accuracy of the predictions.
Will be taken up in Phase 2
Project 11: Swarm dynamics
Recent research interests on unravelling the physics of the locomotion of biological systems like insects, fish and flapping birds stem from the need for designing biomimetic MAVs for surveillance and defence applications. The small size of the individual MAVs imply that these need to be deployed in a swarm for field applications. A key feature in such scenarios is the development of swarm intelligence to ensure that the interactions between the swarm members and the environment enable these autonomous agents to accomplish their mission independently and collectively, without a centralized control. Developments in swarm intelligence rely on adapting the key features of the coordinated movements of schools of fish and flocks of birds, characterized by a lack of a leader (central controller) overseeing the collective dynamics and yet emergence of self-organization patterns, local perception of the environment leading to a certain level of global knowledge by means of effective distributed information sharing [6] and a high degree of adaptation to changing environment. Therefore, there is a need to fully understand the swarm dynamics in biological systems.
Recent studies on the emergence of patterns in the swarms are based on modelling the dynamics of information sharing between the swarm members by adopting network and graph theoretic approaches combined with dynamical models. Alternative approaches that model the swarm as a network of discrete particles with coupled oscillator dynamics have investigated the spatio-temporal dynamical features from the perspective of synchronization. Most of these studies consider the swarm members as discrete particles and essentially adopt a Lagrangian approach to analysis. Resolving the macro properties from hi-fidelity computational models involving the flexible organisms and their interacting effects with their environment can more accurately incorporate a key feature in information sharing in the network. This calls for adopting hybrid models where the agent based modelling approaches will be coupled with higher fidelity continuum model. Such approaches will enable better understanding of the physics of information sharing within the network and their influence of the swarm behaviour.
Applications: The outcome of these studies would be applicable for development of technologies for control of swarms of UAVs/MAVs, crowd control and planning strategies. Will be initiated in Phase 2.


Project 12: Dynamics of social behaviour
The dynamical behaviour of social interactions - like the spread of infectious diseases or fake news - will be investigated by modelling the system through complex network theories. The first phase of the study would focus on using simple mathematical models for information diffusion. Typically, these networks have bipartite nature and the time varying system parameters are incorporated into the network model in the form of noise processes. The dynamics of the network system would be investigated using principles of nonlinear dynamics to investigate the long term dynamical characteristics of the system and the conditions required for attaining the stable equilibrium states. Parametric studies would be undertaken to investigate how the dynamical characteristics change for different standard network topologies and other parameters. It is hoped that the increased understanding of the dynamics will provide insights into countermeasures that can be undertaken to mitigate the harmful effects through social interactions, like spread of infectious diseases or fake news. The second phase of the study would focus on the use of data to construct real world networks and test the theoretical results carried out in the earlier phase. Recent studies [4] have shown that hybrid models based on biomimicry and empirical laws sourced from data analytics accurately capture the collective social interaction behaviour. The methodologies would be investigated both for epidemics as well as social media, networks of which have very different topologies.
Project 13: Causal inference for climate network reconstruction and process-oriented model evaluation
General Circulation Models (GCMs) play a critical role in understanding the past and future climate change under different concentration pathways. Translation of GCM outputs to policy-relevant mitigation and adaptation strategies requires assessing model skills using data science-science methods or physics guided data-driven approaches, often referred to as Process-Oriented Model Evaluation (POME). POME relies on understanding the underlying relationships between the climatological variables (e.g. precipitation, temperature, pressure levels at various geopotential heights) obtained from GCM outputs, observation or proxies. However, while all climate models are based on the same physical principles, there are development-specific choices that lead to significant model differences, in particular related to subgrid-scale parameterisations of clouds, convection and aerosols. These contribute to persistent discrepancies between models and observations and model projections, for example, regarding precipitation changes. Multi-model evaluation and intercomparison is often based on the mean and variance of aggregate quantities, such as temperature, or spectral properties and (auto-)correlation measures. An issue with such metrics is that models can be right for the wrong reasons due to offsetting biases or due to the issue of equifinality. With the growing volume, velocity, variety, and veracity of climate data, complex network-based approaches are gaining popularity. Specifically, the use of statistical causal inference techniques have become pervasive tools in the climate science community for two purposes – discovering new climate events that affect global weather systems and validating theoretical models that produce predictions for centuries ahead.
Several causal inference techniques have been developed since the introduction of the Granger causality, some with a specific focus on climate sciences. Convergent Cross-mapping (CCM) is one such method that was introduced in with an intent to address non-linear dynamical systems that are often encountered in climate sciences. General notions of detecting causal relationships are grounded in modeling causal influence on the effect signal. CCM is unique in the sense that it is based on the idea of recovering the cause from the effect. A variable X is said to cause another variable Y in the CCM sense if the Cross-map Skill (CMS), a linear correlation between measured X and reconstructed X, increases rapidly for small sample sizes and asymptotically converges to a significant value at large sample sizes. Despite its superior ability to detect causal relationships in non-linear settings, there are three shortcomings that this technique suffers from–exorbitant computational costs with scale, a manual inference-drawing mechanism and lack of a formalism for graphical representation from CCM outputs. This project aims to address these limitations and explores the spatio-temporal dependencies of the Indian precipitation system.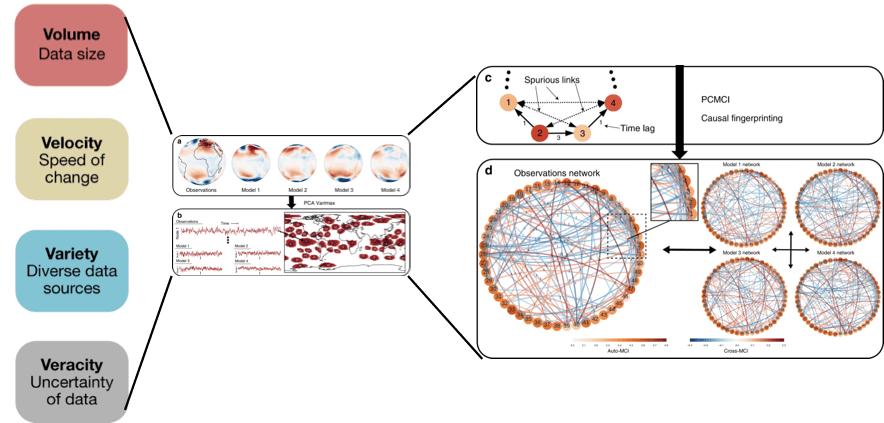
Project 14: Reconstruction of causal dynamical networks of industrial processes
Standard approaches to identifying causal connections and building directed graphical models have used Granger causality-based methods [3-5]. However, such approaches are theoretically unsuitable for engineering systems since the notion of Granger causality [5] and GC-based approaches, that have their roots in econometrics, are built on the premise that the data generating process is purely stochastic, if not stationary. Further, the present methods disregard measurement uncertainties.
It is a fact that these assumptions rarely hold for engineering systems, which are usually described by deterministic differential equations while the measuring mechanism often gives rise to measurement errors. Expectantly, when GC-based methods are applied to these systems, spurious causal relations are identified and biased graphical models are obtained. Non-linearities in industrial processes make this problem even more challenging. There has hardly been any effort in the reported literature on developing a causality analysis framework for identifying network models for deterministic dynamical systems. Recently novel definition of causality for deterministic systems has been proposed and two methods were developed based on multivariate data analysis and delay-based estimation methods for discovering the causal connections. In this project, we aim to extend these ideas to non-linear processes with applications to the reconstruction of dynamical causal networks for processes.
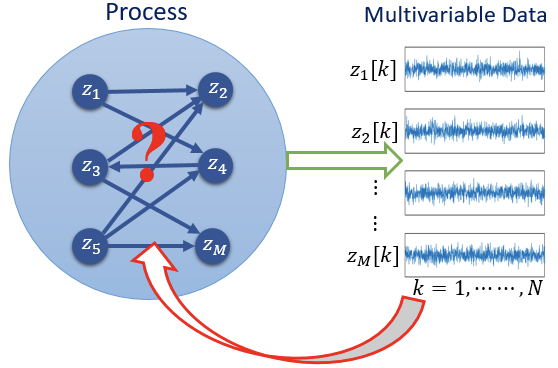
From data to directionality - reconstruction of causal dynamical networks
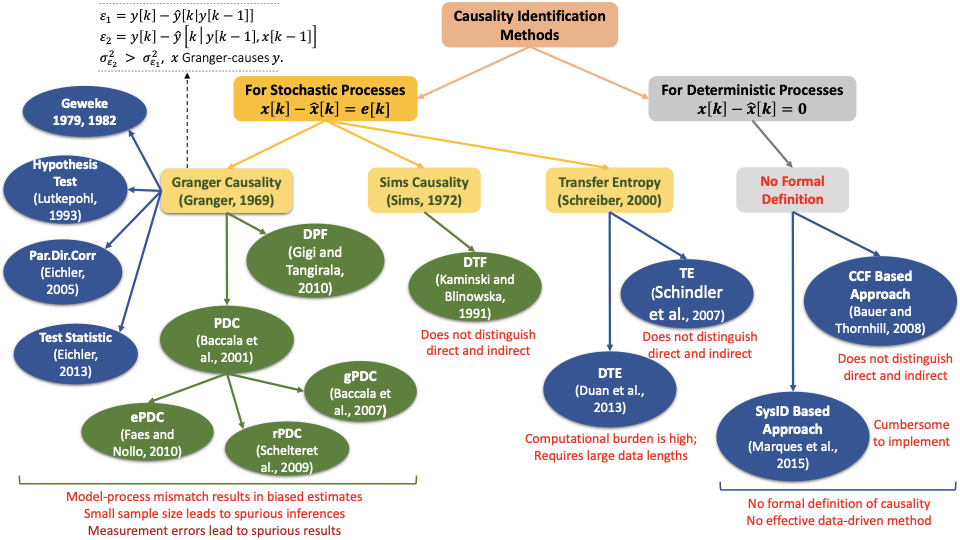
Overview of causal discovery methods for stochastic and deterministic dynamical systems
Expected deliverables of the research
Project 1: Climate Networks
Deliverables
Construction of predictors
Identification of tipping points
Applications to diverse phenomena e.g.
Cyclones, La Nina, El Nina, Monsoon
Machine learning methods for prediction
The deliverables are expected to be in the form of
Journal papers
Conference presentations
Algorithms
Project 3: Stochasticity and noise induced transitions in spatio-temporal systems
- Development of network-based techniques, that are built on rigorous mathematical foundations, for the analysis of such complex systems.
- Investigate reduced order modelling strategies that enable reduction in computational costs without compromising the accuracy of the predictions.
- Development of data driven approaches for estimating model parameters for the above approaches from measurements and observations, so as to be applicable to physical problems.
Project 6: Complex networks for multi-physics systems
- One PhD completion, publications, will explore international collaborations too.
Project 7: Physics-informed machine learning surrogates for complex flows
- Multiple PhD, MS, Mtech and DD projects, publications, collaborations with international colleagues.
Current status
Project 1: Climate Networks
Publications: Precursors of the El Nino phenomenon: R. Sonone and N. Gupte, Physical Review E103,L040301(2021). Signatures of climatic phenomena in climate newtrks: Cyclones, El Nino and La Nina
Infrastructure: Under development
Project 2: Stochastic modelling and machine learning in climate science
- Preliminary work has been started in collaboration with Prof Woosok Moon.
Project 3: Stochasticity and noise induced transitions in spatio-temporal systems
A post doc has been hired who is investiagting effects of noise spatio-temporal systems
Applications - Can be used to predict behaviour of large ordered engineering and natural systems.
Project 4: General oscillatory neural network models to understand fMRI data
The basic model consisting of a few hundred oscillators that can learn multi-channel EEG was just published.
Dipayan Biswas, Sooryakiran Pallikkulath, and V. Srinivasa Chakravarthy. “A Complex-valued Oscillatory Neural Network for Storage and Retrieval of Multidimensional Aperiodic Signals.” Frontiers in Computational Neuroscience, 2021. doi: 10.3389/fncom.2021.551111 Link
This model needs to be expanded to a few thousand oscillators, in which the spatial distribution of the oscillators is constrained by the real brain geometry. The network will be trained to reconstruct brain dynamic signals like high-density EEG, or fMRI signals. The model will also be extended to simultaneously model both EEG and fNIRS data.
Project 6: Complex networks for multi-physics systems
A PhD student already hired working on this project. Basic modeling has been done. A couple of conference presentations have been made.
Applications - Engineering multi-physics systems pertaining to Aerospace, Mechanical, Civil Engineering disciplines, also, engineering systems utilising green technologies as clean energy harvesters from water or wind sources are some of the real-life application areas for the proposed study.
Project 7: Physics-informed machine learning surrogates for complex flows
PhD and MS students already started working on this project. Aim is to understand ML based surrogate modelling, MOR development and future predictions of spatio-temporal states using Autoencoder and Physics based NN. International conference and summer school events are already being participated in.
Applications - Engineering multi-physics systems pertaining to Aerospace, Mechanical, Civil Engineering disciplines, also, engineering systems utilising green technologies as clean energy harvesters from water or wind sources are some of the real-life application areas for the proposed study.
Project 12: Dynamics of social behaviour
- Preliminary studies have been initiated on fake news modelling as well as epidemic modelling using two PhD students.
Collaborations
International collaborators:
Prof Jurgen Kurths link
Prof Madhav Marathe link
Prof Elena Surovyatkina link
Prof Henning S Mortveit link
Prof Didier Lucor link
Prof Murali Damodaran link
Prof Gabriel Mindlin link
Prof Srinivas Aluru link
Prof Ana Amador link
Prof Aravind Srinivasan link
Prof Auroop Ganguly link
Prof Woosok Moon link
Prof Jianxi Gao link
Prof Kirti Rajagopalan link
Dr Sarah Wolf link
Prof Vivek N Prakash link
Prof Zoltan Toroczkai link
Prof Biao Huang link
National collaborators:
- Prof Udit Bhatia link
Societal impact
The primary societal impact of this center shall be felt in the form of bringing scientific rigour to some of the challenging social menaces. The applications of the proposed studies can be useful, for example (but not limited to),
in mitigating the spread of fake news, which poses severe societal challenges. The approaches that will be envisaged and championed in this center, working with the appropriate industry partner, is expected to provide insights on the dynamics of such information spread and identifying timely counter measures.
understanding the viral disease burden at the population scale. In order to understand this burden, it is important to understand the dynamics of aerosol particles in an individual’s deep lung. This personalized approach coupled with a population scale network model will enable accurate modelling of the spread of viral diseases.
investigating the problem of pollutant spread and consequent human behaviour around industrial installations. This requires integrating the outcomes of urban climate modelling with societal behaviour and will help in devising emergency evacuation plans in case of industrial accidents leading to gas leaks.
Many of the big problems faced by the world today are problems in complex systems – this includes for example, the problems of climate change, ecological system and environmental sustenance, complex social systems such as migration, spread of rumours that lead to social unrest and violence, building integrated defence capabilities, complex infrastructural networks. Inability to address these complex issues and challenges faced by the society today would mean that academicians and scientists become irrelevant to the society. This center is positioned to serve this critical societal need by creating an umbrella organization that will bring scientific rigor to hard problems. It is anticipated that financial companies currently impacted by the problems mentioned above, may be interested to support this center through their CSR funds.
The Center would also be focused on training manpower – both at the undergraduate level, as well as in research. This is expected to help build up a new generation of students who would be trained in interdisciplinary studies that encompass disciplines such as science, engineering, biology, medicine, economics and arts. This will enable a future generation of scientists to take up more of these problems. Since the problems proposed to be taken up under this proposal has a very interdisciplinary as well as international flavour, we propose to leverage on this start to ensure that in the long term, the Center would enable further synergy between the natural sciences, engineering, medicine and social sciences leading to addressing more challenging problems and also increase the international footprint in the Cente
Sustenance Statement:
He sustenance plan for this center shall vest on three legs.
First, we shall explore continued funding through industry and government partners, both in India and those from abroad.
Secondly, the primary oxygen for this center is in the form of international visitors who bring fresh perspectives and new ideas. By virtue of the strong pool of international collaborators who are part of this proposal and by virtue of various existing governmental schemes such as VAJRA, GIAN and SPARC, we believe that it will be natural to host dozens of international visitors at the center. In addition, existing frameworks for international collaboration under DST, CSIR, DBT and other government funding agencies shall be exploited.
inally, we will establish linkages with similar centers globally by hosting bilateral seminars and visits (when appropriate). These linkages will systemically place us as an institution to reckon with in this field. Global attention is likely to follow enabling sustainable existence for the center. As a final thought on the sustainability plan, we want to propose that the center will evolve on the long term scale to always remain current in thought and in the set of problems that the center faculty will pursue.
Several industrial partners also have showed interest in the proposed activities of the Center. It is hoped that this can be leveraged for funding at a later stage.
Technical/ Scientific Progress
New work done in the project
There are several projects that are being carried out under this CoE. The list of new publications emerging from the work carried out are listed here
While these publications pertain to completed projects, there are several other projects in which work is going on and is in different stages of completion.
Infrastructure developments
A new 10+1 node high performance cluster, named synchrony, containing 6 CPU and 4 GPU nodes have been installed. The overall capacity of this cluster is about 13 TFlops. An order for the purchase of 3 additional CPU nodes and 1 GPU node has been placed. Apart from this, a high performance workstation from apple has also been bought.
Output
During this period, we have had 8 publications in high quality journals that include Scientific Reports (from nature), Frontiers in Computational Neuroscience, Physical Review E, Journal of Sound and Vibration, Probabilistic Engineering Mechanics, Communications in Nonlinear Science and Numerical Simulations. The details of the publication are available in
As a group, we have conducted 4 international workshops. These include the following:
IRIS webinar on July 2, 2021

Flyers and posters for Workshop on Computational Neuroscience, August 13-15, 2021 website

- Flyers and posters for Networks and Dynamics - An international workshop, August 25-28, 2021 website



- Flyers and posters for Multiphase flows -Advances and future directions, October 28-30, 2021 website

The details of these workshops are available at
Media coverage
A Youtube channel has been initiated for Complex Systems and Dynamics. All lectures, presentations and seminars are being uploaded in the YouTube Channel. Please visit As of today, it is now a repository of 43 one hour lectures and seminars.
Prof Sunetra Sarkar explaining about IDDD on Complex Systems and Dynamics, Science Monitor, Rajya Sabha TV, aired on July 14, 2021
As part of the activities of the pCoE, we have also started a new Inter Disciplinary Dual Degree program on Complex Systems and Dynamics. The first batch contains 13 students. More details about the IDDD program is available here
The IDDD program has received media coverage in Science Monitor, Rajya Sabha TV, aired on July 14, 2021, the link for which is available here
We are maintaining a website at join
Mobility
Visits planned for PI, co-PIs, international collaborators and students (both inbound and outbound)
- A visit is being planned for Prof Srinivas Chakravarthy (co-PI) to University of Virginia, to be hosted by collaboartor and international partner to this pCoE -Prof Madhav Marathe.
- A planned inbound visit of collaborator and international partner of this pCoE, prof Gabriel Mindlin, in february. These visits are subject to covid situation in the world.
Relationship
Industrial Engagement
A discussion has been initiated with Skymet for engaging in collaborative activitiies
University Engagement
Several engagements are currently in progress:
- University of Virginia - lead by prof Srinivas Chakravarthi (Co-PI), international partner Prof Madhav Marathe, area of engagement: computational neuroscience
- University of Beunos Aries - led by prof Neelima Gupte (Co-PI), international partner Prof Gabriel Mindlin, area of engagement: Dynamics of bird song, computational neuroscience
- CNRS France - led by Prof Sunetra Sarkar (Co-PI), international partner Prof Didier Lucor. There are plans of Prof Lucor coming and spending a month in IIT M, area of engagement: Biomimetic flows
- Stockholm University - led by Prof Anubhab Roy (Co-PI), international partner Prof Woosok Moon, area of engagement: Climate dynamics
- University of Miami - led by Prof Anubhab Roy (Co-PI), international partner Prof Vivek Prakash, area of engagement: Biological fluid mechanics
- University of Alberta - led by Prof Arun Tangirala (Co-PI), international partner Prof Biao Huang, area of engagement: System identification and data analytics
- Northeastern University - led by Prof Sayan Gupta (PI), International partner Prof Auroop Ganguly, area of engagement: climate change
- Potsdam Institute for Climate Change - led by Prof Neelima Gupte (Co-PI), International partner Prof Elena Surovyaktina and Prof Jurgen Kurths, area of engagement: climate science and indian monsoon
- Lodz University- led by Prof Sayan Gupta (PI), International partner Prof P Perlikowsky, area of engagement: complex systems and stochasticity.
Updates
Relevant Updates
We have recruited a few PhD students for working on some of these areas. An ongoing post-doc is already working on a problem related to one of the projects, another post-doc is on the process of being hired.